河南省2024届九年级阶段评估(一)[1L]数学试题，目前2024 高中卷子答案已经汇总了河南省2024届九年级阶段评估(一)[1L]数学试题的各科答案和试卷，更多2024 高中卷子答案请关注本网站。

本文从以下几个角度介绍。

1、河南省2023-2024学年度九年级期末考试
2、河南省2023-2024学年度九年级期中检测卷
3、2023-2024河南省九年级数学期中考试
4、河南省2023-2024学年度九年级期末检测卷
5、河南省2023-2024学年第一学期期中教学质量检测九年级
6、河南省2023-2024学年度九年级期中检测卷数学
7、河南省2023-2024学年第一学期教学质量检测九年级
8、河南省2023-2024学年第一学期期末教学质量检测九年级
9、河南省2023-2024学年度九年级期末检测卷数学
10、河南省2023-2024学年度九年级期中检测卷

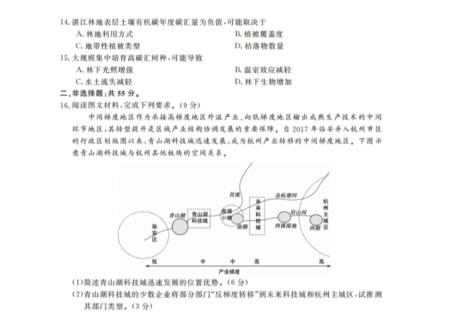
2022届4月高三联合测评（福建）二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分】9.已知等差数列{a:}的前n项和为S.=i+n,公差为d,则2数学A.a1=1B.d=1C.2Sn-am=1+3+5+…+(2n-1)D.S2=2a2+2a,10.在某独立重复实验中，事件A,B相互独立，且在一次实验中，事件A发生的概率为p,事件注意事项：B发生的概率为1一p,其中p∈(0,1)，若进行n次实验，记事件A发生的次数为X,事件B发生的次数为Y,事件AB发生的次数为Z.则下列说法正确的是1.本试卷满分150分，考试时间120分钟A.E(X)=E(Y)B.D(X)=D(Y)2.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码粘贴在答题卡上C.E(Z)=D(X)D.n·D(Z)=D(X):D(Y)的指定位置。11.已知三棱锥P-ABC外接球的球心为O,外接球的半径为4，AB=AC=4,PB=PC,3.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需BC=m(m为正数)，则下列命题是真命题的是改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。A,若m=4V2,则三棱锥P-ABC的体积的最大值为32+16E4.考试结束后，将本试卷和答题卡一并收回B.若P,O,A不共线，则平面POA⊥平面ABC地C.存在唯一一点P,使得OP⊥平面ABC一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是D.m的最大值为4√2符合题目要求的.1.已知集合A={xx-2≤2}，B={1,2,3,4,5},则A∩B12.已知函数f(x)=sin(wr+p,其中w>0.对于任意的p∈（答，受）函数f(x)在区间不A.{1,2,3,4}B.{2,3,4,5}C.{1,2,3}》D{2,3,4}2复致一头（其中为噬数单位在复平面内对应的点在(臣·至)上至少能取到两次最大值，则下列说法正确的是A.第四象限B.第三象限C.第二象限D.第一象限A.函数f(x)的最小正周期小于晋学3.已知双曲线C:等-苦=1（®>0，b>0)的焦距为25，且实轴长为2，则双曲线C的渐近线方程为B.函数f(x)在(0，)内不一定取到最大值A.y=士2xB.y=±√5xC.y=士22D=±9：C.12<a≤号4.已知a为锐角，且sin(a+牙)=sin(a-晋)，则tana=D.函数f(x)在(0，亞)内一定会取到最小值A.√3B.2+√3C.√6D.√6+√3三、填空题：本题共4小题，每小题5分，共20分5.共有5名同学参加演讲比赛，在安排出场顺序时，甲、乙排在一起，且丙与甲、乙都不相邻的概13.已知向量a=(,2)(k>0),b=(3,4),若(a十b)⊥(a-b),则实数=率14.已知奇函数f(x)在[0,1]上单调递增，在(1，+∞)上单调递诚，且f(x)有且仅有一个零A吉BcD号点，则f(x)的函数解析式可以是f(x)=15.已知抛物线y2=21x(p1>0)与抛物线x2=2p2y(2>0)在第一象限内的交点为6.已知某圆台的高为7，上底面半径为√2，下底面半径为2√2，则其侧面展开图的面积为P(x),若点P在圆C:(x-√10)+(y-√10)2=8上，且直线OP与圆C相切，则A.9xB.6√2πC.9√2πD.8√2πp12=7.已知a=eim1e,=e8+。c=eweosg,则16.在处理多元不等式的最值时，我们常用构造切线的方法来求解.例如：曲线y=x2在x=1处A.ab>cB.b>c>aC.ac>bD.c>a>b的切线方程为y=2x一1，且x2≥2x-1,若已知m+n+t=3,则m2十n2+2≥2n一1+2n8.在平面直角坐标系zOy中，点A在x轴上，点B在y轴上，|AB|=2,点C满足AC⊥BC,则1十2t-1=3,取等条件为m=n=t=1,所以m2十n2十t2的最小值为3.已知函数f(x)=点C到点P(W3,1)的距离的最大值为x3-6x2十12x,若数列{an}满足an≤2，且a1十a2十…十a1o=10,则数列{f(an)}的前10项B号和的最大值为；若数列{b。}满足b,≥0，且b1十b2十…十b1o0=180,则数列A.3C.5D.4{f(6.)}的前100项和的最小值为·(本题第一空2分，第二空3分)【高三联合测评·数学第1页（共4页）】【高三联合测评·数学第2页（共4页）】